日志
聖經真的藏有密碼嗎?
|||
|
聖經真的藏有密碼嗎?
魏慶榮
|
|
《聖經》中似乎隱藏了許多訊息,這些訊息是有意安排的?還是文字排列時偶然造成的?對於難以測知的未來,如果有人或有些事物能揭露其奧秘,一定會引起社會上的轟動。而中國預言中最家喻戶曉、膾炙人口的,要屬一千三百多年前,唐貞觀年間袁天罡及李淳風合著的《推背圖》(圖一),書中利用籤詩與卦圖,分別預言唐代以降的國運興亡。
《推背圖》與其他預言書(如:記錄朱元璋和劉伯溫之間對話的《燒餅歌》都有個特色,就是解釋的空間彈往相當大,後人可以根據已經發生的歷史,對相關的文字和圖形,做出合乎己意的註解,因此往往予人所言靈驗的印象(圖二)。因而每個朝代都把《推背圖》列為禁書,但這並不是當政者相信預言的正確性,而是怕謠言四傳,人心浮動,有危及政權的可能。
那麼有沒有一些隱藏的預言,可以用科學的方法來發現與驗證呢?
1994年8月魏茨滕 (D. Witztum;物理教授)、芮普斯(D. Rips;數學教授)及羅森柏格 (Y. Rosenberg;專長為計算)在卡斯(R. E. Kass; Carnegie University 統計系教授及系主任)所主編的期刊《Statistical Science》中發表了一篇名為〈聖經創世記裡的等距字母序列〉 (Equidistant Letter Sequences in the Book of Genesis) 的論文。這篇文章利用統計的方法證明:《聖經》隱藏了許多訊息,而這些訊息是有意安排的,絕非文字排列偶然造成的。而「聖經是否藏有密碼」的這場論戰也正式展開。
《Statistical Science》是 Institute of Mathematical Statistics 的機關期刊之一,與《The Annals of Statistics》、《The Annals of Probability》和《The Annals of Applied Probability》都是一流的國際期刊,當中所刊登的每一篇文章,都經過很嚴格的審查,因此結論相當可靠。 |
對外搜尋關鍵字: .null hypothesis .Ramsey .Erdos .Fisher |
什麼叫做「等距字母序列」(equidistant letter sequence,簡稱 ELS) 1 ?物理學家湯瑪斯 (David Thomas) 以英王欽定版 (King James Version) 的〈創世記〉第三十一章第二十八節為例子:
And hast not suffered me to kiss my sons and my daughters? 把空格和標點符號去掉,合併成字串: AndhastnotsufferedmetokissmysonsandmydaughtersThouhastnowdonefoolishlyinsodoing
然後從「daughters」的 r開始,跳過三個字母,來到「thou」的 o;再跳過等距三個字母,來到「hast」的 s,依此類推。結果得到 ROSWELL(羅茲威爾)這個字。
如果從「thou」的 u開始,跳過十一個字母,得到 f;再跳過等距十一個字母,得到 o。結果, UFO(不明飛行物)和 ROSWELL便同時隱藏在這一段話中了。某些人可能因此推斷,《聖經》早已預示,外星人將降臨在美國新墨西哥州羅茲威爾鎮的沙漠。
這個例子很有趣,可是-《聖經》當初是用希伯來文寫成的 3 ,而非英文。如果要探究《聖經》是否真的藏有訊息,魏茨滕等認為應該回到《聖經》最原始的書寫版本,因此採用了以希伯來文撰寫的〈創世記〉。而他們做的第一件事,就是像剛剛一樣,把空格拿掉、排成一個總共有 78,064個字的長字串,叫作 G, 其中 g1 代表第一個字,而 gr 就是第78,064字。接著他們定義什麼是「等距字母序列」:首先取個整數 d,叫「躍距」(skip),在前面湯瑪斯的例子裡,第一個 d是 4,第二個 d是 12;再來是取字的長度 k,剛才的例子裡,第一個 k=7,第二個 k=3。把這些整理如下: 其中,gn 是起點(start), n可以是小於 r的任意整數,長度 k、躍距 d也沒有特別的限制;至於形成的字是否有意義,則是另外一回事。這樣就能構成所有的等距字母序列了。
等距字母序列是一位叫魏斯曼德(Weissmandel)的猶太教士(rabbi,音譯拉比,故簡稱猶太教士為拉比)發現的,也有可能是更早的拉比,把羊皮紙捲在柱子上讀時,偶然間發現直讀或斜讀的字串,有時有特殊意義,而這種字串都是 ELS。
不過魏茨滕如何從 ELS找出一個非比尋常的隱藏訊息呢?為此他們做了一個實驗,從《以色列偉人百科全書》(Encyclopedia of Great Man in Israel),找出三十二位拉比,記下他們的名字 xi(這本書所記載的拉比生活在 9到 18世紀末,離〈創世記〉所寫的時代,已經有好幾千年了),及其出生死亡日期 yi。由於希伯來文裡沒有阿拉伯數字,都是用字母來表示數目的。所以剛剛的字串,也可以用來表示這些日期。接著對這個二維的字串( xi, yi),定義一個距離 c( xi, yi)(定義的方法過於細節,不在此詳述,有興趣的人可以去看看相關的論文)。結果發現,等距字母序列的資料庫裡,每個拉比的名字,跟他出生月日的距離非常接近,就像先前看到的 ROSWELL跟 UFO也是非常接近(其實就在同一行裡);因此他們覺得其中必定有特別的意義,絕不是靠運氣、巧合得來的。而這個想法正是最有意思的地方!首先要確認的一件事就是:這些人名、出生日期是否可以弄混?因為如果弄混了,可是對定義出來的距離遠近,並沒有太大差別的話,就表示結果是偶然發生的;如果有顯著差別的話,就表示這不是純靠運氣就能解釋的現象了。因此他們便利用統計檢驗的方法,看看這樣的配對究竟是不是「純屬偶然」。 |
這些討論到目前為止都是很學術性的,不過我們的故事才剛剛開始哩!事實上,這篇文章早在1987年就送到《美國科學院會誌》(Proceedings of the National Academy of Sciences of the United States of America) 去發表了,其中一位經手的是 Persi Diaconis。 Diaconis 年輕時是位有名的魔術師,現在則是哈佛大學的統計學家。他在更早的時候(1986年),就跟三位作者聯繫過,有可能就是作者在文章中提到的,建議他們做對照實驗的科學家。
在生物相關的研究裡,常常要做對照實驗。舉個簡單的例子來說,感冒吃藥會痊癒,但是也有人不吃藥也會好,那要如何驗證藥是不是真的有效?通常會找兩組感冒的人,一組吃藥,一組沒有吃藥,或是為了避免心理因素的影響,而給他們吃並不含藥效的「安慰劑」,然後做比對,看看有吃藥的是不是比較好。而這 個建議也要求他們去找一個「安慰劑」,於是他們就找了《戰爭與和平》當對照本。這本書是俄國文豪托爾斯泰寫的,有希伯來文的翻譯本,但因為原來是用俄文寫的,因此可以當做「安慰劑」。 對照本取的是書最前面,字數跟〈創世記〉一樣的部分。結果發現,對照本在相同的檢定下,並不顯著,也就是說它的 p 值大於0.05。而這相對加強了「ELS 的相近,並不是一時好運」的結論-然而美國科學院的會誌還是拒絕了這篇投稿,於是他們就改投到《Statistical Science》。
《Statistical Science》找了三位審稿人,一般而言審稿人都是兩位,不過這個題目太奇怪了!令人非常困惑,特別是〈創世記〉的創作距今隔了三千多年,其間都沒有提到別的事情,到現在才發現它跟近代的事物有關,這不是非常奇怪的事情嗎?所以還是小心為上!於是這些審稿人自己也去重新分析,看看作者的統計方法合理嗎?然後再檢查他們的計算。最後的結論是,雖然有一點出入,不過效果依然存在。也就是說,顯著性跟沒顯著性,依然不變。因此《Statistical Science》的主編卡斯就接受了這篇文章,並且在編輯前言說,這就留給讀者當作是一個挑戰性的謎題,希望讀者能夠去解決。而這個謎題一直到下個事件發生前,全世界好像都不太感興趣。不過站在作者的立場來說,既然1994年到1997年間,都沒有人發表任何評論,他們自然會認為文章的想法以及結論已經是被接受了。這就是我們的序幕,也就是故事的開始。 |
故事第二景,「聖經密碼」出現。如果稍微注意一下,剛剛那些作者的結論是很中性的,只是說 ELS 的靠近,不是因為運氣好而產生的;但是它並沒有告訴我們,到底是由什麼產生的。由於作者具有宗教的背景,是傳統的猶太教徒,當然心裡想的是一種宗教的結論。可是在統計學上,在虛擬假設不被接受的情況下,要是另一個假設(對立假設),如果沒有寫清楚的話,那麼虛擬假設縱使不對,但到底什麼是對的,仍然不是很確定。因此,「歸之於上帝」也只是其中一種講法而已。不過,對宗教信仰者來說,在他寫下這樣的文章時,暗地裡恐怕早就有那樣的對立假設存在了吧! |
接著下一個故事就要跳到1997年5月28日,《紐約時報》(New York Times) 登了一幅全頁廣告,廣告是宣傳一本書,書名叫做《The Bible Code》,也就是《聖經密碼》。這一本書的作者叫卓思寧 (Michael Drosnin),是《華盛頓郵報》和《華爾街日報》的前記者,他花了五年的功夫調查,然後自己做實驗寫成這本書。這本書的廣告以及書的內容大致是這樣的:三千年來,《聖經》的密碼隱藏未解,現在已經被電腦解開來了,而且可以預示一切末來。作者卓思寧說,根據這個密碼顯示,以色列總理拉賓的名字和暗殺連在一起;而且事實上,他在1994年9月就寫過一封信給拉賓,告訴他這個可能性,可是拉賓沒有理會他,而後在1995年1月,拉賓就死於刺客之下。這是這本書中最轟動的一件事,而且作者是迫不及待、開宗明義的,在第一章裡就提到這件事,因為這是他自己親身經歷過的事件,是由他自己解出密碼、預知的大事。
除此之外,這個廣告以及這本書反覆提到,揭示密碼的方法是經過期刊認可的,特別是有同儕審核的期刊所認可的。事實上,卓思寧也求教於不少數學家,而他表示每位數學家都覺得,這一切的確證明了密碼存在。不過卓思寧更厲害的一點是,說完〈創世記〉裡藏有密碼,能夠預告人類的命運後,接著又說在〈摩西五經〉(也就是舊約的前五卷:〈創世記〉、〈出埃及記〉、〈利未記〉、〈民數記〉跟〈申命記〉)中,他都發現藏有聖經密碼,當中傳達的訊息除了拉賓被刺殺外,還包括美國甘迺迪和林肯兩位總統,以及印度總理甘地遇刺的事件,日本神戶、美國舊金山的大地震、世界末日與廣島原子彈轟炸等,種種過去與未來發生的大事件。
而這幾卷經文其實可以說是猶太民族的史記,〈創世記〉記載了上帝造人、亞當與夏娃,以及諾亞方舟的故事;〈出埃及記〉描述早期猶太人定居埃及,和摩西如何與埃及法老鬥爭,然後帶領人民離開埃及的經歷;〈利未記〉是摩西到西奈沙漠的途中,以色列部落利未人如何支持他清教的經過;〈民數記〉記述以色列人在西奈沙漠漂泊和初到巴勒斯坦的生活史;〈申命記〉則記載摩西如何將政權傳給約書亞的事。而許多人可能對〈申命記〉特別感興趣,因為媒體過去一直傳說,我們的李前總統是摩西,而陳水扁總統是約書亞,這個典故就在〈申命記〉裡。 |
再回到聖經密碼裡,更令人驚訝的是,卓思寧除了〈摩西五經〉外,在舊約的〈以賽亞書〉內,也找到密碼。一個眾所皆知的現象是,一旦有人對一個現象做推廣,大家也都會跟著做推廣。因此呢,信奉基督教的人也在找,看看新約裡是不是也藏了密碼。結果,不但是信仰猶太教或基督教的人在找「聖經密碼」,連信奉回教的人也在找,整件事情一下子就宣揚開來了,尤其是在《紐約時報》刊登的整版廣告,加上這些慫人聽聞、預知興亡的詞句,其中的新聞價值非常高。因此 CNN、《紐約時報》、《時報雜誌》(Time Magazine)、《新聞周刊》(News Week)都特別介紹,接著連一般的「脫口秀」,如 Today Show及 Oprah show也都出現了相關話題。而一旦在美國造成這麼大的轟動後,很多種語言的翻譯本也就跟著出現了。台灣的《聖經密碼》就是由杜默先生翻譯的。
除了多種語言的暢銷書以外,「聖經密碼」的相關產品很快也隨著出現了。首先是有關別的隱藏訊息,以及新的密碼的書,接著是電視記錄片,連電影也有拍攝的計畫,此外如果你想「自己」解密碼的話,也有商業的軟體提供。有興趣的話,還可以上網站,鍵入「Bible Code」去搜尋,很快就有一大串相關的項目條列出來了,其中包括各種論戰、宗教團體的解說 …等,顯然「聖經密碼」這件事情已經造成全世界轟動。 |
針對這麼轟動的事,自然引起了不少反響。正如前面所提過的,虛擬假設不成立,的確表示當中「有東西存在」,不過這東西是密碼嗎?還是有別的理由造成這樣的現象呢?接著就來看看數學家是如何解釋的。
數學家於是翻出了拉姆西 (Ramsey) 定理,這個定理的完整敘述相當拘泥形式,抽象難懂,幸好有位有名的數學家艾狄胥 (Paul Erdös) 4 ,喜歡用所謂的「宴會問題」來解釋。所謂的「宴會問題」是說,一個宴會裡如果有六個人,是不是一定會存在三個人彼此之間互相認識,或彼此之間一個也不認識的現象?這個答案是肯定的。彼此認識或完全不認識都是結構 (pattern),當人數愈來愈多的時候,許多奇奇怪怪的結構就會跟著出現。就像繁星滿布的夜空,會看到許許多多的星座一樣。因此這個定理給我們的教訓,正如美國數學家默慈金 (Theodore S. Motzkin) 所說的:「完全的無秩序是不可能的。」但是這只是觀念上的啟發,說明像〈創世記〉那樣字數龐大的著作,存在密碼是有可能的:不過針對原來的問題,這並沒有證明太多事情,不見得是我們要的答案。
另外一方面,芮普斯-原來論文的三個作者之一,希伯來大學 (Hebrew University) 的數學教授,由於一些未說明的原因,認為未來事件不可能預測,而且認為卓思寧有些譯解的密碼在統計上的意義不顯著,也就是說,對應的 p 值沒有小於0.05。卓思寧在寫聖經密碼的時候,前前後後訪問了芮普斯好幾次,沒想到在面對批評時,他們彼此意見在第一步,就不完全一致。
接著有許多人發現,卓思寧用的方法和等距字母序列那篇論文的方法相比,相當不嚴密。不少人(例如我們一開始就提到的湯瑪斯)用相同的方法,很容易發現到處都藏有密碼,就如英王欽定版的《聖經》裏,可以找到 UFO 一樣,這下子整個懷疑都出來了。而卓思寧面對這些批評,又是如何回應的呢?在《新聞周刊》的一次訪問裡,他說:「假如我的批評者 ,能夠在《白鯨記》(Moby Dick)裡,找到某位總理被刺殺的密碼訊息,那麼我就會相信他們。」這對批評者來說,是個挑戰!而這場戰爭到這個時候,已經是相當白熱化了。
澳洲國立大學(Australia National University)的一位計算機教授馬凱(Brendan McKay),就接受這個挑戰,找到了底下印度總理甘地被刺的「訊息」(圖三),並且把它放在自己的網站上。
圖三中直行的 IGANDHI,第一個 I 是他的名字 Indira 的縮寫,按著是甘地 (Gandhi)。按著橫行是 the bloody deed。死亡的契約,預示著甘地是會被殺的。事實上,馬凱不但找到一位總理 ,他還在《白鯨記》找到 Abraham Lincoln(林肯)、拉賓、甘迺迪…等名人被刺殺的訊息,用的是跟卓思寧一樣的方法。哇!這下子麻煩了,似乎到處都藏有密碼,是不是生活周遭都布滿天機,等著我們用電腦去解讀呢?這位馬凱是個很有趣的人,他說,基督教徒也一直在尋找密碼,不過他們想找的是有關耶穌基督降臨的訊息;那麼是不是我們也來試試看!而這回他用的是〈但以理書〉,因為卓思寧在《聖經密碼》中提到這是一本「封印之書」,預告著「彌賽亞來臨的日子」,而耶穌向來都被視為是彌賽亞的。馬凱依照魏茨滕等人的方法,考慮了一些關鍵字詞,像 son of god,去進行分析,結果發現耶穌跟 son of man 較靠近。這下子耶穌由「神之子」變成「人之子」,整個論戰也跟著變得混沌、局勢不明了。 |
事情演變到此,卓思寧似乎略居下風,但是這件事並沒有完全解決,原因在於對原先魏茨滕等人的那一篇〈聖經創世記裡的等距字母序列〉並沒有直接的推翻。因為這三個人的確很用心在設計他們的實驗,而且很仔細地做統計分析;而他們也認為卓思寧有些地方太寬鬆,做了一些統計不顯著的結果。因此想反駁他們,一定要提得出道理,說明他們的作法到底有那裡出了問題,否則光是用那些圖表的方式或是拉姆西定理,恐怕還是沒有辦法讓人心服口服;更何況芮普斯也一直表示,只有〈創世記〉裡有聖經密碼,想反駁這一點,也勢必要回歸到原先的這一篇文章來。
而經過同儕審核的期刊文章,還是要由期刊文章,而且最好是由同一期刊的文章來反駁,比較有公信力與說服力。1998年馬凱與兩位希伯來大學的學者,巴希蕾(Bar-Hillel)及巴納丹(Bar-Natan),首先在一通俗性的統計期刊《Chance》,針對魏茨滕等的文章做全面的反駁,裡面沒有太多技術性(統計)的探討,但是描述了整個事件的來龍去脈,攻擊言辭猛烈,並且宣稱在《戰爭與和平》的希伯來文版,也可以發現密碼,這跟魏茨滕等人的論文結果相反。接著在1999年,馬凱等三人再加上希伯來大學的數學教授卡萊(Kalai),在《Statistical Science》發表了一篇學術文章:〈解決聖經密碼的疑惑〉(Solving the Bible Code Puzzle),為《Chance》的文章提供了統計學上的依據。他們在這篇文章中表示,魏茨滕等人在1994年發表的那一篇文章有相當嚴重的缺陷,特別是實驗的設計和數據的收集。有什麼問題呢?這時就要回過頭來看看,統計裡對實驗設計有哪些要求。 |
統計學中討論實驗設計時,通常都會提到:找尋最佳生產配方的工業實驗設計,以及找尋新藥的藥物試驗設計。關於後者,由於過去幾十年來對臨床實驗新藥的經驗,學界和醫界已經訂立了相當嚴格的標準,這些標準的規範,都寫在議定書 (protocol) 裡。首先要知道,做醫學實驗,或藥廠試驗新藥前,一定要先寫議定書,而且必須在議定書批准後才能開始進行。通常議定書裡必須寫明實驗的目的是什麼,整個的設計是什麼,又要如何執行。以下所列的十四個項目,是波克 (S.J. Pocok) 在《臨床試驗》(Clinical Trials) 中列舉的: (1)背景與一般目的(Background and general aims)。 (2)特殊目的(Specific objectives)。 (3)選取病人的標準(Patient selection criteria)。 (4)療程(Treatment schedules)。 (5)評估的方法(Methods of patient evaluation)。 (6)試驗設計(Trial design)。 (7)病人的註冊及隨機分配(Registration and randomization of patients)。 (8)病人的同意(Patient consent)。 (9)研究需要的數量(Required size of study)。 (10)試驗進展的監控(Monitoring of trial progress)。 (11)表格與數據的處理(Forms and data handling)。 (12)協議的偏離(Protocol deviations)。 (13)統計分析的規畫(Plans for statistical analysis)。 (14)行政責任(Administrative responsibilities)。 以下選出跟密碼問題有關的幾項,稍作說明。
首先,當然要說明實驗的背景和目的是什麼。魏茨滕等人的主要目的,是要證明上帝在〈創世紀〉裡藏有密碼。論文的特殊目的就是想證明,拉比的名字與其出生日期很靠近,並不是偶然的事件。
其次的幾項與病人的處理有關,其中病人的選取對應到論文裡拉比的選取。而魏茨滕等人是用什麼標準來選取這些拉比的?這牽涉到許多事情,包括拉比名字的拼法,如何依此去估算出前面所提到的距離,其中的細節留待後面再敘。在醫學實驗裡,如果選取的病人一開始就很虛弱,且併發症不少的話,那麼即使藥再靈,效應恐怕都不會很好;但是如果病人的病症很輕微,看來很強壯的話,那麼「藥到病除」和「不藥而癒」的情況都有可能。因此病人和拉比的選取,會直接影響所有的分析結果。
再來是討論試驗的設計,而這關係到之後要如何做實驗。例如魏茨滕是透過配對,以及對照實驗的方法來進行的。對照實驗是一種比較實驗,除了處理因素(如藥效或上帝預示)外,其他可能會影響實驗結果的因素都必須控制得完全一樣。所以魏茨滕等人利用《戰爭與和平》做對照實驗時,採用希伯來文版,而且將字數選得一樣多,就是這個目的。另外。有人可能聽過「雙盲設計」(double blind design),主要是說,如果要實驗兩種可能的藥物時(當然包括安慰劑),那麼除了病人本身不知道他吃的是什麼藥,免得心理作用之外,連醫生也不知道病人服用的是不是安慰劑,以免醫生因為知道病人「有吃藥」的前題,而使診斷不自覺的傾向有效的判斷,認為病人會因此變得比較好。因此雙盲(或者叫雙瞞)的主要目的,也是要求在實驗的過程中,盡可能避開人為的偏見。而在對病人次序的編排上,譬如單數吃藥,雙數吃安慰劑等,也有可能產生這種不自覺的偏見 5 ,所以有必要弄亂吃藥者的編排(隨機化),使其不是順著一個固定的模式進行。由於隨機的安排,病人有可能因此沒吃藥。所以必須讓病人事先同意整個過程。
還有,這樣的實驗到底需要多少病人,也是一個很有趣的問題。例如。魏茨滕的實驗選了三十二個拉比,這樣夠不夠?少一點是否也能證明相同的結論?或者為了周全,必須把整個百科全書裡的人都選進來?這點很值得思考,表格和數據處理看起來不起眼,其實非常重要。例如許多表格常要填寫出生年、月、日,而論文中拉比的資料只有出生的月和日,並不包括年,處理這樣的資料時就要特別小心。此外,萬一實驗與議定書有所偏差時,例如應該進來的病人沒有進來,需要的樣本少一個時怎麼辦?諸如此類的事情,在議定書裡都要表示清楚。
第十三項規定怎麼做統計分析,這一項很清楚不用多說。最後是責任的問題。換句話說,這洋洋灑灑的十四項,其實只有一個目的,就是所有實驗的進行,都應該是在嚴格的規範下操作的,否則很可能會出問題。 |
瞭解實驗設計後,再回過頭來看看馬凱他們的批評:第一、魏茨滕等人所用的統計方法,如果一小部分的數據稍微變動一下,就會很敏感。第二、最大的麻煩出在拉比的稱呼,以及它的拼法如何選擇上。以我們的現任總統為例,可以稱呼他陳水扁,陳總統水扁,陳水扁先生或是阿扁,甚至還有種種別名,到底要選哪一個?在西方社會裡,還有縮寫的問題哩!
魏茨滕實驗所分析的拉比,是根據一位名叫 Havlin的教授所準備的名單。但是另一位研究拉比的學者 M. Cohen卻說,這種取法是沒有科學根據的,完全是不一致的,而且是一個隨意選取的結果。他同時也準備了一分名單。不過更好玩的是,另一位學者認為,這兩分名單「一樣令人訝異!」由此看來,光是名字這一部分,仔細推敲就產生很大的問題了,更何況猶太人對日、月還有各種不同的講法,就如同我們有一月、正月和元月等講法。所以在議定書裡,諸如此類的規定就要事先制訂好,否則就有很大的伸縮空間;一旦有了伸縮空間,解釋就多,往往就無法控制了。但也有可能殊途同歸,達到相同的結果。
因此,下一步要問的就是,假如真有這樣的自由度可以發揮的話,它所產生的後果是什麼?馬凱等人依照上述的自由度,應用在《戰爭與和平》的版本上,把那些拉比的名字稍微變動一下, 得到的數據結果卻是 p <0.05。換句話說,《戰爭與和平》從沒有顯著的結果,變成有顯著結果。
再來,就〈創世紀〉的實驗來說,它原先的方法為什麼是對的?是不是它的自由發揮得太過度了呢?馬凱等人認為是的。而且他們還測試了很多小小的變動,譬如把出生的年分加進去、用別的稱呼等,結果發現大部份的結果都變弱了,有些變得不太顯著,有些甚至已經不顯著了。種種現象,似乎指向作者對數據的選擇,有固定的偏好,像是去挑撿一些特別的拉比,才得到這樣的結果。馬凱甚至表示,魏茨滕他們其實作了一些「調整」(tuning)。這種現象的另一種說法是「直覺的統計期望」。意思是說,當你知道一個現象的理論結果是什麼的時候,做出來的實驗結果往往就會是如此;因為有了這樣的心理傾向,就會產生了一些自覺或不自覺的「調整」行為。所以受到這樣心理影響的實驗報告,就會過於完美,必須特別小心這樣的結果是不是真的。
這一類的事件在統計界也發生過,其中最有名的,就是統計學家兼遺傳學家費雪(Fisher)對孟德爾(Mendel)碗豆實驗的數據所產生的懷疑。費雪甚至表示,當初孟德爾可能為了理論,調整了數據;原始的數據,不應該那麼漂亮。不過還好,最後孟德爾的理論是對的。這表示,即使數據真的是製造出來的。結果也不見得是錯的;但是實驗的結果那麼好,總會令人懷疑這些數據是被動過手腳的。因此調整的另外一個講法,就叫「動手腳」。不過費雪的懷疑是有其理論基礎的,因為這樣完美的結果表示,它的結果是不允許抽樣帶來的合理誤差。事實上,每個樣本都會對應一個統計量,通常不同樣本的統計量,彼此並不完全相同。就像用望遠鏡去量測天空中某個星球的距離,量測次數一多時,即使再怎麼努力調整儀器,結果多少都會有一些起伏的。這種起伏就是抽樣誤差造成的,也有人歸因於廣義的雜訊 (noise)。真正的度量難免會摻雜著噪音,而有噪音的數據,其所對應的定 p 值就不應該太小。而魏茨滕的 p 值小到 10-6(百萬分之一),因而讓人對於其數據的取得產生一些疑問。 |
最後,馬凱等人又從歷史的角度,再度批評了一番。由於目前這個《聖經》的版本,並不是一天定下來的,它與《孟子》、《老子》這些書一樣,都是源遠流傳的,創作始於兩、三千年前。以1947到1951年間,在死海的西北端發現的《死海古卷》來說,那是一個寫在羊皮上,相當古老的的《聖經》原文,很可能是目前所知最古老的《聖經》書籍。書裡的〈以賽亞書〉相當完整,還有很多〈創世記〉的片段,但大都是殘卷。後來的《聖經》版本很可能是根據這些殘卷再修正的,因此,經文如果有密碼,這個密碼也不可能從最原始的版本流傳至今。因為經文在流傳的過程,難免會經過刪減和插增, 如果先前定義的躍距 d很小的話,選出的 ELS不變的機會就很大,密碼就不會被刪掉;可是如果 d很大的話,只要中間刪掉一個字母,就不再是一個完整的 ELS。例如,卓思寧在找出拉賓被剌這個密碼時用的 d=4,772,在間隔這麼長的字串中,要保證沒有被插入或刪除實在很難。所以從文獻流傳的觀點來看,也沒辦法保證密碼不是後天造成的。
最後馬凱他們下了兩個結論。首先,他們認為這篇文章不是故意找一個檢定方法來配合數據的。也就是說,並不是數據已經在那邊,然後再故意找一個方法將推論做得很好。舉例來說,如果要用平均值(方法),來代表王永慶先生與筆者的財富狀況(數據),那麼筆者當然就會顯得很有錢,可是那個平均值一定不能代表筆者的收入,這個方法只是故意要造成筆者很有錢的結論。這就是所謂的,用方法來配合數據,雖然數據是客觀的,方法卻是為了產生特定的效果而制定的。馬凱他們表示,目前這篇文章並不是這樣的,它是透過拉比的選取,因而調整了數據來配合這個檢定的。就像是前述王永慶和筆者的例子,把王永慶換成一位比他窮一點的人,再用一位比筆者富有一點的人來取代筆者,使兩者間的收入差異不大,這時用平均值來做代表,自然就合乎統計的道理了。
第二個結論則是全篇文章的總結。他們認為並沒有證據顯示,有辦法從 ELS找到密碼。拉比的名字跟生日這些配對的安排相近與否,純屬機運。主編卡斯也對此做了回應,他在馬凱等人的文章之前是這麼介紹的 :「…正如他們所下的結論,這個謎題的確像是解決了。」《Statistical Science》似乎有意為這場論戰譜上休止符,而不想再爭辯下去了。 |
| 結語 |
讀者如果學過計算機或是統計學,最近一定聽過一個名詞。叫做 data mining,也就是到 data 裡去採礦,因此有人將它翻譯成「資訊探勘」 6 。要採什麼礦呢?就是在一個龐大的數據裡,找出它的規律性來。例如,如果對超市裡進、出帳的項目瞭解清楚的話,就會知道哪些產品,在什麼季節,顧客會比較需要,然後就可以在適當的時間,多進一些這方面的產品;同時從這些龐大的數據裡,瞭解顧客消費的規律性,就能企畫出有效率的行銷手法,這些就是資訊探勘的意義。可是,資訊探勘處理的數據通常是相當龐大的,而且絕對比一般應用時碰到的例子項目來得多,數量來得大。尤其是像銀行一天的進出,筆數相當驚人,因此不用計算機處理不行。於是就有很多軟體公司,看準這點商機,開始販售整套資訊探勘的套裝軟體,這時候要特別小心。以「聖經密碼」的例子來說,它雖然有一個相當龐大的數據,卻也有辦法找到一個很像很有規律性的東西來,但是不是真的有那樣的規律性呢?則是值得深思的。所以當各位忙著「探勘」時,不妨學習它的正面意義,不過同時也要小心,你所採到的是金沙呢?還是石頭呢?是不是該找位統計學家問問看呢?
 圖一:《推背圖》的第一象甲子,書中利用籤詩與掛圖,分別預言唐代以降的國運興亡。
圖一:《推背圖》的第一象甲子,書中利用籤詩與掛圖,分別預言唐代以降的國運興亡。  圖二:《推背圖》中的第四十二象乙己,就有多種解釋。
圖二:《推背圖》中的第四十二象乙己,就有多種解釋。 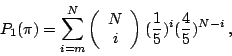
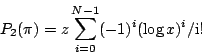
 圖三:馬凱教授在《白鯨記》中找到甘地被刺的訊息。
圖三:馬凱教授在《白鯨記》中找到甘地被刺的訊息。 

